再帰データ型

整数や浮動小数だけの計算には限界があります。高度なプログラムを開発するには、高度なデータ構造が必要です。MLでは、すでに出てきた(x, y)のような組の他に、「xまたはy」のような型を定義することができます。型の再帰も可能です。これらを用いると様々なデータ構造を表すことができます。

たとえば、整数を葉とする「木」は次のように定義できます。

# type int_tree = Leaf of int | Node of int_tree * int_tree ;;

type int_tree = Leaf of int | Node of int_tree * int_tree

これは「int_treeはLeaf（葉）またはNode（枝）であり、Leafは整数、Nodeはint_treeとint_treeの組からなる」という意味の定義です。

たとえばLeaf 123という式は、整数123を持つ葉が一つだけの木を表します。

# Leaf 123 ;;

- : int_tree = Leaf 123

Node(Leaf 123, Leaf 456)だったら、枝が一つあって、整数123を持つ葉が左に、整数456を持つ葉が右にある、という木になります。

# Node(Leaf 123, Leaf 456) ;;

- : int_tree = Node (Leaf 123, Leaf 456)

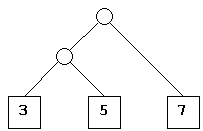
Node(Node(Leaf 3, Leaf 5), Leaf 7)という式は、下のような木を表すことになります。ただし○が枝、□は葉を表すものとします。

もう少しややこしい例として、とにかくランダムに木を作る関数は、次のように書くことができます。

# let rec make_random_tree () =

if Random.int 2 = 0 then Leaf(Random.int 10) else

Node(make_random_tree (), make_random_tree ()) ;;

val make_random_tree : unit -> int_tree = <fun>

# make_random_tree () ;;

- : int_tree = Node (Leaf 8, Node (Node (Leaf 8, Leaf 3), Leaf 1))

# make_random_tree () ;;

- : int_tree = Leaf 3

# make_random_tree () ;;

- : int_tree = Node (Node (Leaf 3, Node (Leaf 4, Node (Leaf 0, Leaf 2))), Leaf 8)

make_random_treeは引数が特に要らないので、ダミーの値()を受け取ることに気をつけてください。そもそも木というデータ構造自体が再帰により定義されているので、再帰関数によって非常に自然な記述が可能となっています。

次へ進む